前言
我最近在想,究竟漩渦該怎麼畫?
如果只是一圈圈漸漸變大,看起來不太有漩渦的感覺
應該是遙遠處變化平緩,愈靠近變化愈快才對吧?
於是,我試著在紙上畫一個這種圖形:
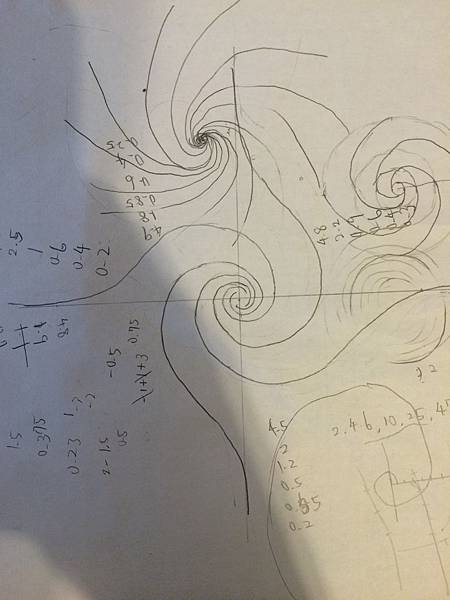
中間那個
然後,我畫了垂直兩條線,X軸 Y軸
用尺量出各個焦點跟中心的距離,然後取平均
發現6, 10, 25 很像是指數函數!
假設漩渦上的一點 P 的極座標是 (R, θ)
(R 是P 點和中心的距離,θ 是P 點和X 軸的夾角)
推測 R 對於 θ 是指數函數!
Geogebra
所以打算用Geogebra 來畫畫看漩渦的圖形
想法是一個圓上有個點一直在遶,然後圓的半徑指數得變大
這樣一來,X軸 Y軸 的交點就會指數的變大了!
於是我用了一個拉桿=a,作自變數
然後在底下打了個公式: b=e^a
然後,在圓的方程式上,將 Circle[A,B] 改成 Circle[A,b]
之後,把a 值調成 "每次增加0.01",速度調成 "0.5",範圍是0~5
在圓上,上下左右各設了四個點,每個點圍繞的速度忘記設多少了 ><
反正,是以角度為單位圍繞,不是以弧長為單位
讓那四個點大略相差90 度圍繞
畫出來的圖長這樣:

真的有漩渦的感覺!
之後調了各種a 的速度,畫出來了各種圖形:
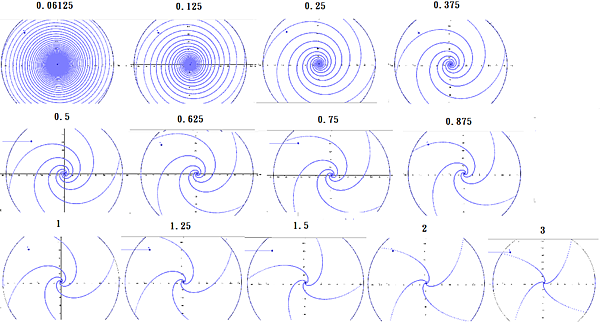
看得出來,最像漩渦最漂亮的,是 0.375~0.875 左右~~
事後分析這種 直觀 的作法,
θ=c1 t
R=e^(c2 t)
所以,R=e^(θ c2/c1),
R(θ) 確實是指數函數
(但當時沒想這麼多啦XD)
文章標籤
全站熱搜
